Maria and I are hosting a Halloween party this year, which means we are doing a lot of cleaning, decorating, cooking, and purchasing large quantities of alcohol. Maria has a polaroid-type camera and likes to have it available for guests to take pictures during the party. I will usually hang up some sort of clothesline on the wall so guests can post photos during the party and take them home at the end.
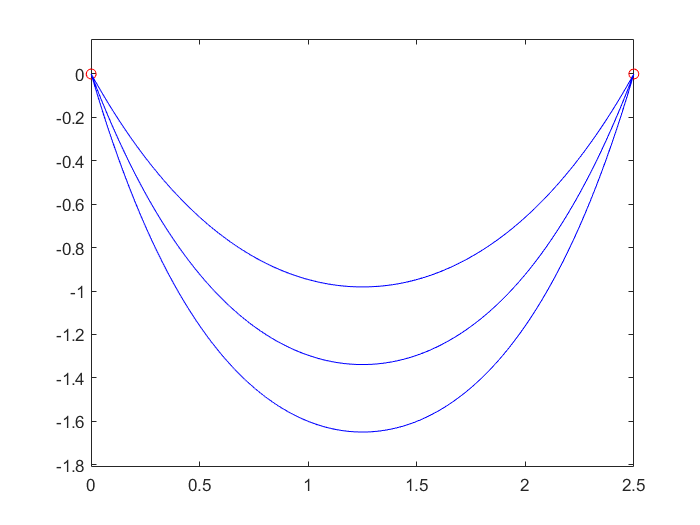
In previous apartments, I’d just make one long clothesline to maximize the number of photos that could be posted. However in our current apartment, the ideal clothesline location is quite narrow and a single clothesline would only be able to hold a handful of photos. The obvious solution would be to put up more clotheslines but I didn’t want to put so many nails in the wall. The next alternative is then to have multiple clotheslines suspended from 2 common points. This solution would work but requires some knowledge of what the string lengths should be to space the photos evenly. The string available for this task was quite fibrous and I did not want to have to tie/retie the strings multiple times, so a wrote a quick matlab script to calculate the string lengths to ensure the spacing was even.
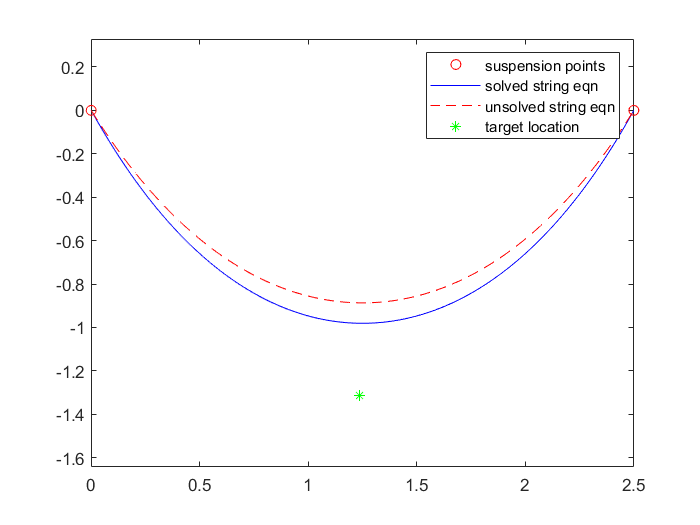
The catenary curve is a generally a good model for the shape of a string suspended at two points. The key underlying assumptions for this model are non-elasticity and uniform density of the string. The objective is to generate catenary curves given the coordinates of the suspension points and the string length. The difficulty with catenary curves is that you can’t analytically derive the curve that meets all those criteria; it must be numerically solved. Luckily, someone in the matlab community has already created a function to do this.
I setup another iterative solver on top to increase the string length until the desired spacing was reached. The amount of increase on each iteration was proportional to the deviation of the current iteration from the setpoint. Not the most elegant, but it gets the job done.