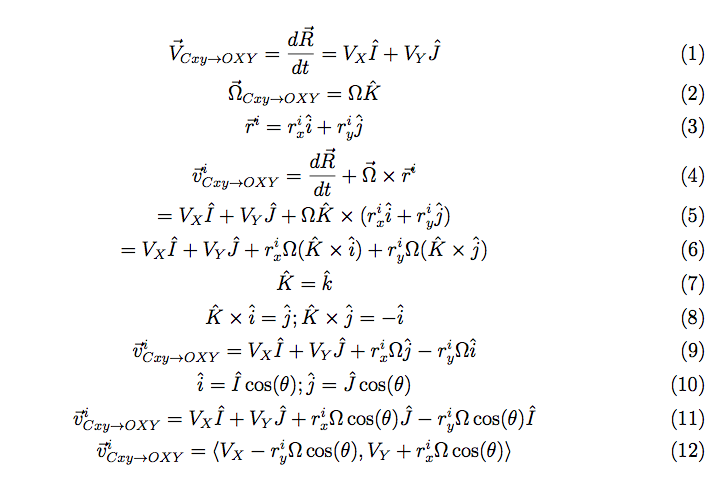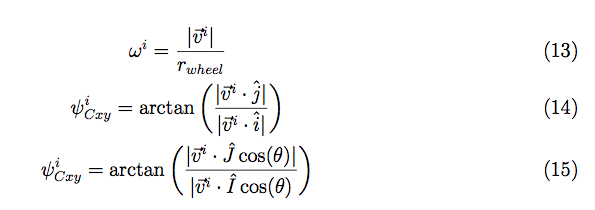After many discussions, our group has decided that four-wheel drive simply does not permit adequate control of the robot for aligning with the circuit breaker cubicle. So we are reverting to our original drive train choice: swerve drive. Swerve drive is a holonomic locomotion system in which each wheel can pivot about its own vertical axis. Using a swerve drive, the robot will strafe sideways along the face of the circuit breaker cubicle, detecting the edges of the cubicle and using those edges to laterally align the robot. Then, the robot will perform an angular alignment to the face of the cubicle, and advance forward to extract the breaker. The angular alignment and subsequent forward motion would not have been possible with a four-wheel drive system; as the translation and rotation of the robot are coupled.
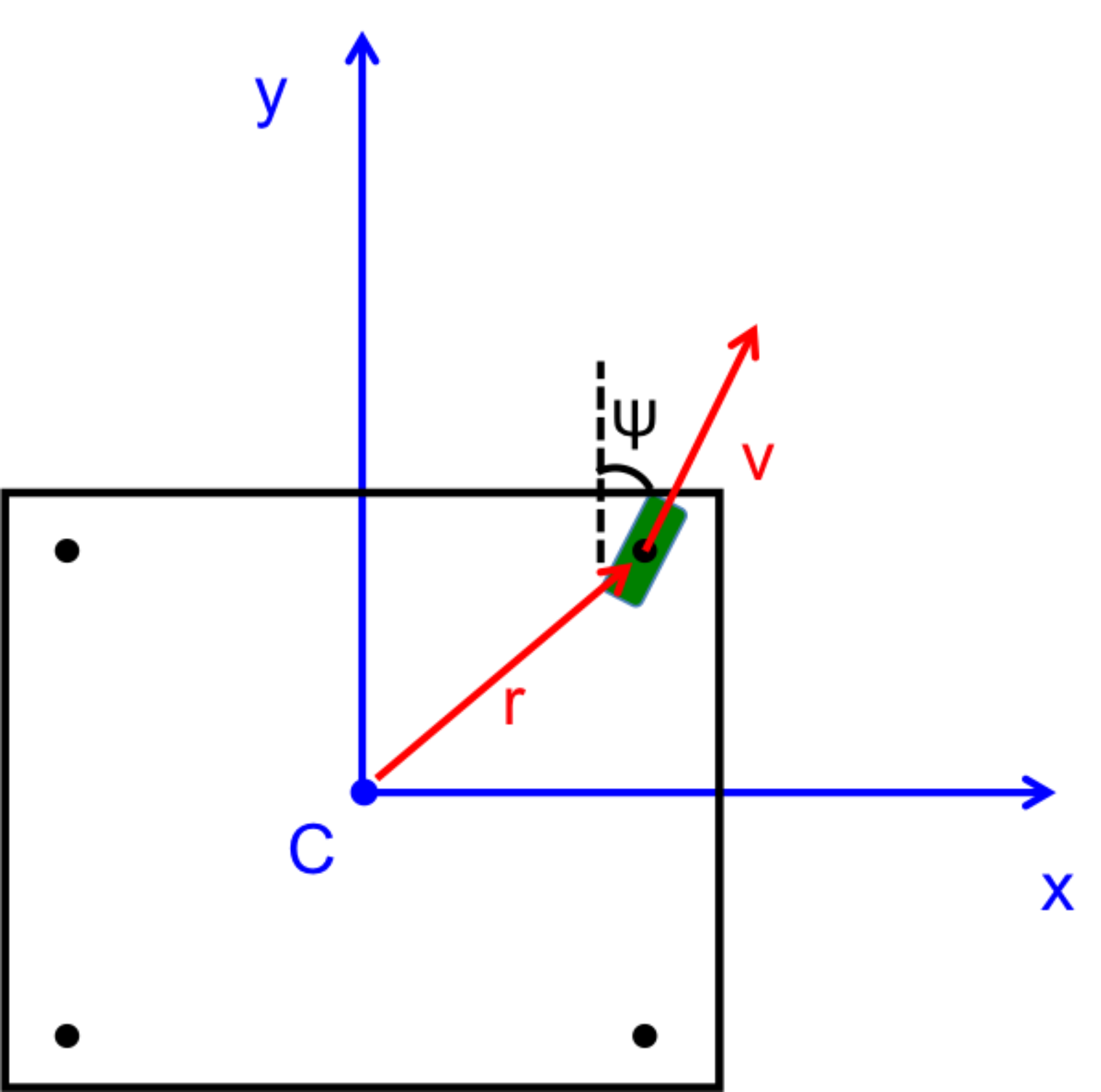
I derived the inverse kinematics of the robot for our computer engineers to use in their control algorithms. The derivation is quite simple mathematically, but it can easily get confusing to understand from a physical sense. I like to imagine what I would experience if I were sitting on the different points where the wheels are located on the robot. This helps me to see why certain terms are in the resulting equations and verify if the results make sense.
PDF derivation of the kinematics.